Page Not Found
Page not found. Your pixels are in another canvas.
A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.
Page not found. Your pixels are in another canvas.
About me
This is a page not in th emain menu
Short look for the master integrals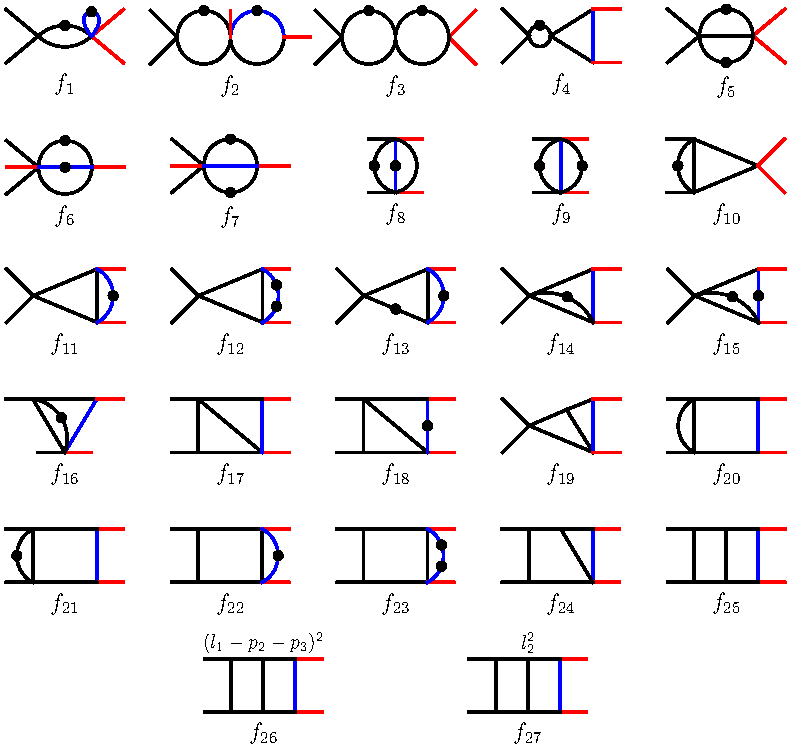
The more loops and legs, the more complicated it gets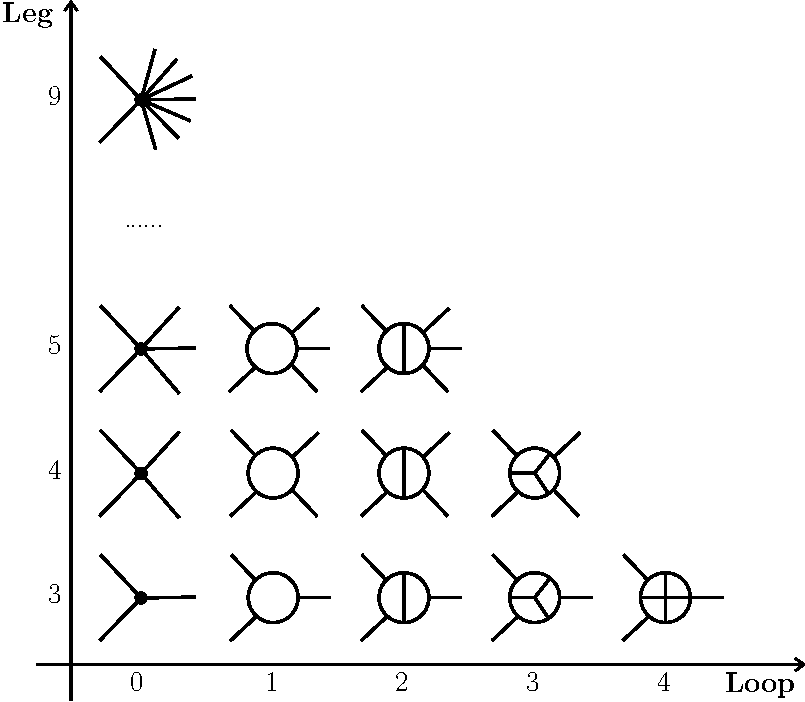
Published in unknow, 2023
We calculate the two-loop mixed QCD\(\otimes\)EW corrections for the charged Higgs boson pair production within the framework of four types of Two Higgs Doublet Models (THDMs) with the \(Z_2\) symmetry. We analyze in detail the dependences of our results on physical parameters, including the charged Higgs mass, \(\tan\beta\), the scattering angle, and the colliding energy. It is noticeable that the mixed QCD\(\otimes\)EW relative correction is independent of the scattering angle due to the topology of Feynman diagrams at \(O(\alpha\alpha_s)\). Numerical results in most allowed regions of four types of THDMs are provided in the density plots on the \(m_{H^{\pm}}\)-\(\tan\beta\) plane. For type-I and type-X, the mixed QCD\(\otimes\)EW relative correction varies slightly near \(1\%\) except in the vicinity of resonance. For type-II and type-Y, the corrections increase consistently in large \(\tan\beta\) region and reach up to \(11.5\%\) at \(\tan\beta = 50\). We also compute the \(O(\alpha)\) corrections to obtain the corrected cross section up to \(O(\alpha\alpha_s)\). The numerical results show that the corrected cross section can be larger than \(80\ \mathrm{fb}\) in some parameter space region for type-I and type-X THDMs.
Recommended citation: Zhi-Xing Zhang, ... , Wen-Jie He, ... . https://arxiv.org/abs/2312.17207
Published in Dec., 2024
The discrepancy between the CDF measurement and the Standard Model theoretical predictions for the \(W\)-boson mass underscores the importance of conducting high-precision studies on the \(W\) boson, which is one of the predominant objectives of proposed future \(e^+e^-\) colliders. We investigate in detail the production of \(W\)-boson pair at \(e^+e^-\) colliders and calculate the mixed QCD-EW corrections at the next-to-next-to-leading order. By employing the method of differential equations, we analytically compute the two-loop master integrals for the mixed QCD-EW corrections to \(e^+ e^- \to W^+ W^-\). By utilizing the Magnus transformation, we derive a canonical set of master integrals for each integral family. This canonical basis fulfills a system of differential equations where the dependence on the dimensional regulator, \(\epsilon\), is linearly factorized from the kinematics. Finally, these canonical master integrals are given as Taylor series in \(\epsilon\) up to \(\epsilon^4\), with coefficients written as combinations of Goncharov polylogarithms up to weight four. Upon applying our analytic expressions of these master integrals to the phenomenological analysis on \(W\)-pair production, we find that the \({O}(\alpha\alpha_s)\) corrections hold substantial significance in the \(\alpha(0)\) scheme, especially in the vicinity of the top-pair resonance (\(\sqrt{s} = 2\, m_t\)) induced by top-loop integrals. However, these corrections can be heavily suppressed by adopting the \(G_{\mu}\) scheme.
Recommended citation: Zhe Li, ... , Wen-Jie He, ... . https://arxiv.org/abs/2401.01323
Published in May, 2024
首先我们在第一章回顾了标准模型的建立以及利用费曼图进行微扰论计算的方法, 指出费曼图中涉及到的多圈费曼积分是微扰论计算的一大难点。 第二章中我们介绍了费曼积分的相关概念和目前与之相关的研究技术。 维数正规化方法可以将积分中的发散表征出来, 积分结果可以表示为$\epsilon$的洛朗级数展开的形式。 通过将费曼积分变换到特定表示下,我们能够直接计算出积分的结果, 或者得到某些可以利用的性质。 我们分别介绍了Schwinger参数表示、费曼参数表示以及Baikov表示。 费曼参数表示被广泛地应用于直接计算费曼积分的结果, 并且已经有许多实用的程序包被开发出来; 而Baikov表示则更多地用于分析积分性质,例如利用其来寻找正则基。 除了直接计算费曼积分,目前更加有效的方法是构建费曼积分关于运动学变量 的微分方程组,通过求解方程组进而获得费曼积分的表达式。 我们介绍了此类方法的基本概念和一些简单的例子, 并结合所给例子,展示了正则微分方程具有的便利性。 我们还介绍了如何利用费曼积分的cut,并且说明了利用其寻找正则基的可能性。 但是对于多圈多外腿以及多标度的积分,该方法应用时很难找到正则形式。 另外在具体工作中,还存在许多需要引入根式来构建正则微分方程系统的情况。 同时有理化根式通常只有在根式数量少、根式形式简单的情况下完成, 大量根式将导致我们难以利用已知的特殊函数GPL来写出积分的表达式。 对于轻夸克对湮灭产生玻色子对的过程, 已有不少唯象学方面的研究。 在所有带质量玻色子对产生中,该过程具有最大的产生截面, 被广泛应用于研究电弱相互作用的规范对称性以及电弱对称性的破缺机制。 我们不仅能够利用其对\Wbo 玻色子质量进行精确测量, 还能够对反常三规范玻色子耦合顶点进行检验。 由于w玻色子对的产生过程为Higgs粒子衰变过程的不可约本底, 其在寻找Higgs玻色子的过程中也有着不可或缺的作用。 研究轻夸克对湮灭产生玻色子对的过程的解析计算对于理论预言也是十分重要的方面。 但是由于其涉及的主积分中传播子所带标度较多, 完整的解析结果仍然处于探索中。 在本文第三章,我们计算了该过程中的平面主积分, 该过程中存在三个需要被计算的双圈平面拓扑结构。 由此我们建立了三个独立的微分方程系统, 在构建正则微分方程的过程中我们遇到了根式的有理化问题, 以及线性微分方程求解的问题。 最终写出了这些主积分的表达式, 其中有三个主积分属于椭圆sector, 最终的结果不仅包含GPL及其一重积分, 还有关于椭圆积分的迭代积分。 最后我们通过与现有数值方法作比较,检验了结果的正确性。 而如何高效获得这些出现的特殊函数的数值解,也是目前急需的技术, 只有攻克这些技术难题,我们才能系统且高效地得到更高圈、更多标度费曼积分的解析结果, 推动解析计算在高能唯象理论中更深层次的发展。 不止如此,研究高阶微扰论修正中费曼积分也能加深人们对于量子场论中数学原理的理解, 为理论发展提供有力的支撑。
Recommended citation: Wen-Jie He http://maplerrr.github.io/files/hwj-thesis.pdf
Published in Dec., 2024
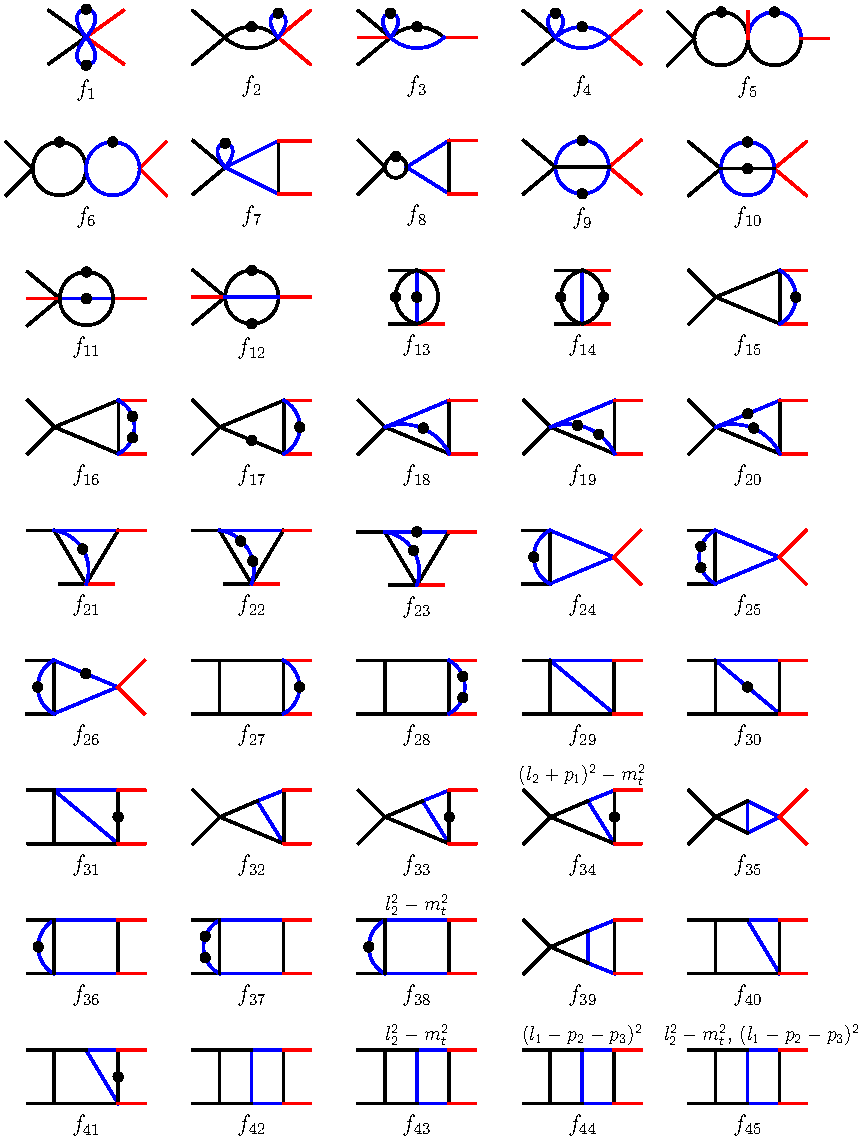
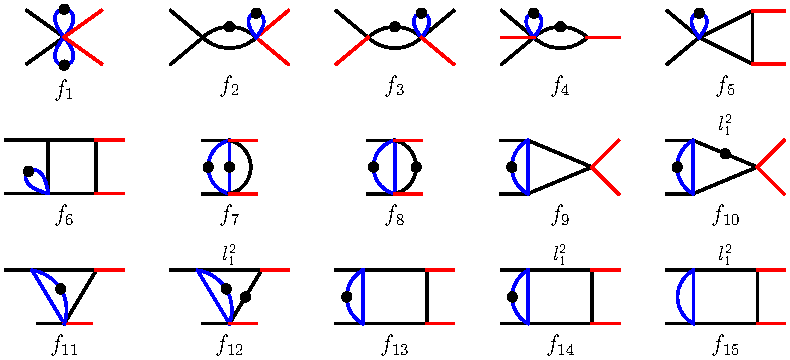
The planar two-loop scalar Feynman integrals contributing to the massive NNLO QCD corrections for W-boson pair production via quark-antiquark annihilation can be classified into three family branches, each of which is reduced to a distinct set of master integrals (MIs), totaling 27, 45 and 15, respectively. These MIs are analytically calculated using the method of differential equations, with solutions expanded as Taylor series in the dimensional regulator \(\epsilon\). For the first two family branches, the differential systems can be successfully transformed into canonical form by adopting appropriate bases of MIs. This enables the MIs of these family branches to be expressed either as Goncharov polylogarithms (GPLs) or as one-fold integrals over GPLs, up to \(O(\epsilon^4)\). In contrast, the differential system for the third family branch can only be cast into a form linear in \(\epsilon\) due to the presence of elliptic integrals. The solution to this linear-form differential system is expressed in an iterated form owing to the strictly lower-triangular structure of the coefficient matrices at \(\epsilon\)=0. Our analytic expressions for these MIs are verified with high accuracy against the numerical results from the AMFlow package.
Recommended citation: Wen-Jie He, ... https://arxiv.org/abs/2409.08879
Published:
You can learn about my specific work through the slide because my paper is controlled by my boss. The paper for this work is not finished, because some optimizations are underway.
Published:
The roots involved roots appear in this work. It’s interesting!
You can learn about my specific work through the slide because my paper is controlled by my boss. The paper for this work is not finished, because some optimizations are underway.
Undergraduate course, University 1, Department, 2014
This is a description of a teaching experience. You can use markdown like any other post.
Workshop, University 1, Department, 2015
This is a description of a teaching experience. You can use markdown like any other post.